In the third part of this JavaScript kinetic scrolling series, the so-called snap to grid feature is demonstrated. The implementation is rather straightforward, it is a matter of figuring out where the scrolling should stop and then adjusting that target position to the intended location.

The second part of the series discussed the scrolling deceleration technique by using an exponential decay concept. With a flick list, this means that the list will slow down and stop at some point, depending on the launch velocity at the moment the user releases the grip. It turns out that this also becomes the important key to implement snap to grid.
Note that the exponential decay curve permits us to know about two things (1) when the scrolling will stop (2) where it will stop. As soon as the launch velocity is known, these two values can be computed analytically. This is very powerful, in particular since the final stop position can be adjusted right away. For a quick live demo, go to ariya.github.io/kinetic/3 (preferably using your smartphone browser), flick the list, and see how it always stops to align the color entry to the overlaid slot.
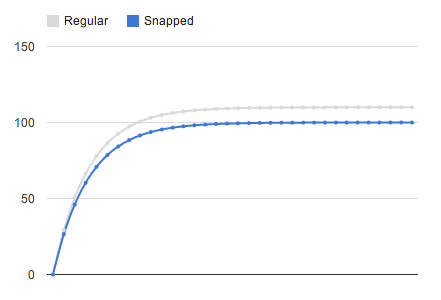
The following diagram illustrates the concept. Without any snap to grid, the curve of the scrolling position as a function of time is depicted in the gray line. Let us assume that the final position will be at 110 px. If we know that the snapping grid is every 25 px, then that final position needs to be adjusted either to 100 px or 125 px. Since the former is the closest, that will be the ultimate final position and the deceleration will follow the curve colored in blue.
The relevant code for this feature can be seen in the repository github.com/ariya/kinetic. Really, it is not much different than the code shown already in the previous second part. The new addition is this following fragment:
target = Math.round(target / snap) * snap;
The variable snap here stores the row height of each item (it is computed once during the initialization). If you already familiarize yourself with the exponential decay implementation, target contains the final scrolling position when the deceleration finishes. Without snapping feature, we don’t tweak this value. When we want to adjust the final scrolling position to be magnetically anchored to nearest snapping location, then we simply change this value.
Also, observe that there is no requirement that snap has to be a constant. A list with non-uniform row height can still enjoy snap to grid feature. All we need is an array of possible values for the final position and every deceleration target must be modified to the closest value. In case you study physics, this is quite similar to the idea of discrete packets of electromagnetic energy in quantum mechanics.
In some libraries which implement kinetic scrolling, snap to grid is implemented by continuously tracking the scrolling position. When it is about to stop, then the position is adjusted to move to the closest possible position based on the grid distance. Not only this results in a more complicated code, such an approach has a major drawback. In some cases, the list can overshoot before it bounces back and therefore it does not demonstrate a smooth scrolling effect at all. With the analytical technique described here, this awkward effect will not happen at all. As always, a proper solution often comes with the cleanest implementation!
What will be shown in the fourth part? Let’s keep it as a surprise!