This will be the first part of a series of weekly blog posts where I outline the steps necessary to create a math expression evaluator using ECMAScript. By the end of the series, you expect to know the magical machinery which can understand and compute the result of the following expression:
sin(pi/4) * sqrt(2) + 41
It is not targeted for hard-core computer scientists who likely already passed Compiler Techniques 101 with flying colors. This is geared more towards those who have a strong interests in the world of parsing but can’t afford the time to complete a whole course.
As with any educational tutorial, don’t expect this stuff to be in the production grade. For clarity, sometimes I also choose the most illustrative way to achieve a certain thing, it may not be the most optimal and fastest approach. For a start, I intentionally avoid regular expressions although in some particular real-world cases that’s exactly what you should use.
Note: if you are eager to know the entire code, head to my TapDigit project page. The project is rather unfinished and not documented well, thus I advise you to stick with this detailed explanation. The code in the project is however very useful since it is more complete than various simplified fragments presented here. For your reference, there is also a summary page describing the expression syntax.
This Part 1 is about lexical analysis, i.e. breaking down a math expression into a list of tokens. A function that does this is often called a lexer, a tokenizer, or a scanner.
We need to define the types of the tokens. Since we deal with simple math expression, all we really need are number, identifier, and operator. Before we are able to distinguish a short string as one of these token types, we need some helper functions (they are self-explained):
function isWhiteSpace(ch) {
return (ch === 'u0009') || (ch === ' ') || (ch === 'u00A0');
}
function isLetter(ch) {
return (ch >= 'a' && ch < = 'z') || (ch >= 'A' && ch < = 'Z');
}
function isDecimalDigit(ch) {
return (ch >= '0') && (ch < = '9');
}
Another very useful auxiliary function is the following createToken, mostly to avoid repetitive code at the later stage. It basically create an object for the given token type and value:
function createToken(type, value) {
return {
type: type,
value: value
};
}
As we iterate through the characters in the math expression, we shall have a way to advance to the next character and another method to have a peek at the next character without advancing our position.
function getNextChar() {
var ch = 'x00',
idx = index;
if (idx < length) {
ch = expression.charAt(idx);
index += 1;
}
return ch;
}
function peekNextChar() {
var idx = index;
return ((idx < length) ? expression.charAt(idx) : 'x00');
}
In our expression language, spaces do not matter: 40 + 2 is treated the same as 40+2. Thus, we need a function which ignore white spaces and continue move forward until there is no such white space anymore:
function skipSpaces() {
var ch;
while (index < length) {
ch = peekNextChar();
if (!isWhiteSpace(ch)) {
break;
}
getNextChar();
}
}
Supposed we want to support standard arithmetic operations, brackets, and a simple assignment, then the operators which we need to support are + - * / = ( ). A method to scan such an operator can be constructed as follows. Note that rather than checking the character against all possible choices, we just use a simple trick utilizing String.indexOf method. By convention, if this scanOperator function is called but no operator is detected, it returns undefined.
function scanOperator() {
var ch = peekNextChar();
if ('+-*/()='.indexOf(ch) >= ) {
return createToken('Operator', getNextChar());
}
return undefined;
}
Deciding whether a series of characters is an identifier or not is slightly more complex. Let’s assume we allow the first character to be a letter or an underscore. The second, third, and subsequent character can be another letter or a decimal digit. We disallow a decimal digit to start an identifier because it gives a confusion with a number. Let’s begin with two simple helper functions that do the above checks:
function isIdentifierStart(ch) {
return (ch === '_') || isLetter(ch);
}
function isIdentifierPart(ch) {
return isIdentifierStart(ch) || isDecimalDigit(ch);
}
The identifier check can now be written as a simple loop like this:
function scanIdentifier() {
var ch, id;
ch = peekNextChar();
if (!isIdentifierStart(ch)) {
return undefined;
}
id = getNextChar();
while (true) {
ch = peekNextChar();
if (!isIdentifierPart(ch)) {
break;
}
id += getNextChar();
}
return createToken('Identifier', id);
}
Since we want to process math expressions, it would be absurd not to be able to recognize numbers. We want to support a simple integer such as 42, a floating point like 3.14159, and also numbers written in scientific notation like 6.62606957e-34. A skeleton for such a function is:
function scanNumber() {
// return a token representing a number
// or undefined if no number is recognized
}
And here is the breakdown of the function implementation.
First and foremost, we need to detect the presence of a number. It’s rather easy, just check whether the next character is a decimal digit or a decimal point (because .1 is a valid number).
ch = peekNextChar();
if (!isDecimalDigit(ch) && (ch !== '.')) {
return undefined;
}
And if that is the case, we need to process each following character as long as it is a decimal digit:
number = '';
if (ch !== '.') {
number = getNextChar();
while (true) {
ch = peekNextChar();
if (!isDecimalDigit(ch)) {
break;
}
number += getNextChar();
}
}
Since we want to support a floating-point number, potentially we will see a decimal point coming (for example, for 3.14159, up to now we still process 3 only). If that is the case, we need to loop again and process all the digits behind the decimal point:
if (ch === '.') {
number += getNextChar();
while (true) {
ch = peekNextChar();
if (!isDecimalDigit(ch)) {
break;
}
number += getNextChar();
}
}
Scientific notation with exponent means we will see e right after. For example, if we are supposed to scan 6.62606957e-34, we are only up to 6.62606957 now. Thus, we need to process more digits after the exponent sign. Note that there can be a plus or a minus sign as well.
if (ch === 'e' || ch === 'E') {
number += getNextChar();
ch = peekNextChar();
if (ch === '+' || ch === '-' || isDecimalDigit(ch)) {
number += getNextChar();
while (true) {
ch = peekNextChar();
if (!isDecimalDigit(ch)) {
break;
}
number += getNextChar();
}
} else {
throw new SyntaxError('Unexpected character after the exponent sign');
}
}
The exception is needed because we want to tackle invalid numbers such as 4e.2 (there can not be a decimal digit after the exponent sign) or even just 4e (there must be some digits after the exponent sign).
Wrapping up our number lexing yields (combining all the bits and pieces above into a complete scanNumber function is left as an exercise for the reader):
return createToken('Number', number);
If we want to consume a math expression and produce a list of tokens represented by the expression, we shall have a function which recognize and get the next token. This is rather easy now since we have three individual functions which can handle a number, an operator, or an identifier.
function next() {
var token;
skipSpaces();
if (index >= length) {
return undefined;
}
token = scanNumber();
if (typeof token !== 'undefined') {
return token;
}
token = scanOperator();
if (typeof token !== 'undefined') {
return token;
}
token = scanIdentifier();
if (typeof token !== 'undefined') {
return token;
}
throw new SyntaxError('Unknown token from character ' + peekNextChar());
}
And that’s about it!
Note: a much improved variant of the above “let’s try each scan function one by one” is actually doing a look ahead and decide which scan function to pick. This is left as an exercise for the reader.
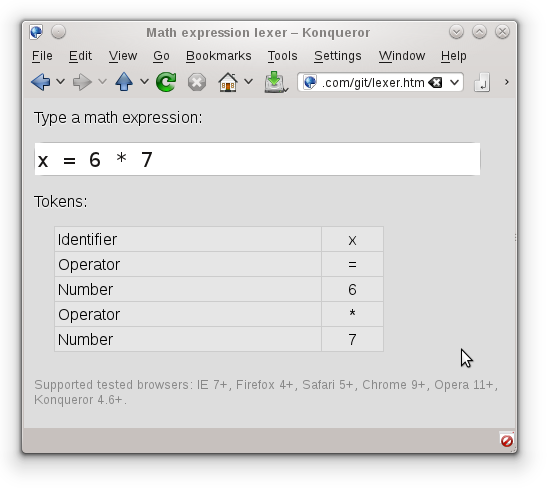
For a live demo, go to ariya.github.io/tapdigit/lexer.htm (works also on most smartphone browsers). You can enter an arbitrary (but valid) math expression and the demo will break it down into tokens and present them in a table.
In the next installment, I’ll cover the next stage after this: parsing the expression to produce the syntax tree. Enjoy and see you next week!
Update: The second part is now online! It’s about syntactic analysis, i.e. building the parser.
Another update: The final part, about the actual interpreter, is now available.