This is the final part of my weekly series on how to write a math expression evaluator in JavaScript. If you haven’t do so, it is recommended that you read the first part (on lexical analysis) and second part (on parsing and syntax tree) before digesting this blog post.
Note: If you want a different take on this subject, have a look at Dmitry’s Essentials of Interpretation.
First, let me show you again an exemplary syntax tree:
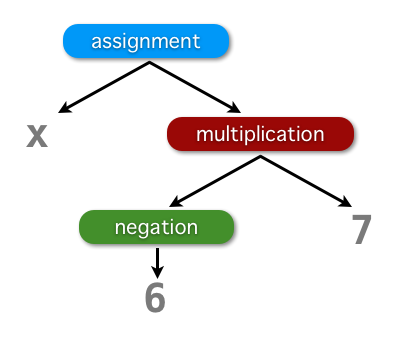
If you are about to compute the expression represented by the above syntax tree, it is actually as easy as walking through every node in the tree (depth-first traversal) while doing a certain operation associated with the node. For a binary operator, it means we just need to add (or substract or multiply or divide) the two values obtained from each child node. This is basically the so-called abstract syntax tree interpreter because we interpret the operation represented by each syntax node.
Before we move on, let’s see first the JSON version of the syntax tree depicted in the above picture:
{
"Expression": {
"Assignment": {
"name": {
"Identifier": "x"
},
"value": {
"Binary": {
"operator": "*",
"left": {
"Unary": {
"operator": "-",
"expression": {
"Number": "6"
}
}
},
"right": {
"Number": "7"
}
}
}
}
}
}
The code to interpret this JSON-formatted tree is quite straightforward. Let’s start from the leaf, such as a number (we assume from here onwards that node points to the current node we need to evaluate):
if (node.hasOwnProperty('Number')) {
return parseFloat(node.Number);
}
For a unary operation node, we need to evaluate the child node first and then apply the unary operation, either + or -:
if (node.hasOwnProperty('Unary')) {
node = node.Unary;
expr = exec(node.expression);
switch (node.operator) {
case '+':
return expr;
case '-':
return -expr;
default:
throw new SyntaxError('Unknown operator ' + node.operator);
}
}
Binary node is handled similarly, we just need to process both child nodes for the left and right side of the operator:
if (node.hasOwnProperty('Binary')) {
node = node.Binary;
left = exec(node.left);
right = exec(node.right);
switch (node.operator) {
case '+':
return left + right;
case '-':
return left - right;
case '*':
return left * right;
case '/':
return left / right;
default:
throw new SyntaxError('Unknown operator ' + node.operator);
}
}
Before we continue to tackle variable assignment, let’s take a step back and see the concept of evaluation context. For this purpose, we define the context as an object that holds the variables, constants, and function definitions. When we evaluate an expression, we also need to pass a context so that the evaluator knows where to fetch the value of a variable, store a value to a variable, and invoke a certain function. Keeping the context as a different object promotes the separation of logic: the interpreter knows nothing about the context and the context does not really care how the interpreter works.
In our evaluator, the simplest possible context is:
context = {
Constants: {},
Functions: {},
Variables: {}
}
A slightly more useful context (and thus can be used as a default one):
context = {
Constants: {
pi: 3.1415926535897932384,
phi: 1.6180339887498948482
},
Functions: {
abs: Math.abs,
acos: Math.acos,
asin: Math.asin,
atan: Math.atan,
ceil: Math.ceil,
cos: Math.cos,
exp: Math.exp,
floor: Math.floor,
ln: Math.ln,
random: Math.random,
sin: Math.sin,
sqrt: Math.sqrt,
tan: Math.tan
},
Variables: {}
}
We still do not have any variables (because the context is freshly created), but there are two common constants ready to use. The difference between a constant and a variable in this example is very simple and obvious: you can not change a constant or create a new one, you can do both with a variable.
With the context and its variables and constants ready, now we can handle identifier lookup (e.g. in an expression like x + 2):
if (node.hasOwnProperty('Identifier')) {
if (context.Constants.hasOwnProperty(node.Identifier)) {
return context.Constants[node.Identifier];
}
if (context.Variables.hasOwnProperty(node.Identifier)) {
return context.Variables[node.Identifier];
}
throw new SyntaxError('Unknown identifier');
}
Assignment (like x = 3) works the other way around, though we have to ensure that we only process variable assignment and not constant override:
if (node.hasOwnProperty('Assignment')) {
right = exec(node.Assignment.value);
context.Variables[node.Assignment.name.Identifier] = right;
return right;
}
Finally, the remaining function node is handled as follows. Basically the function arguments (if any) are prepared in an array and then passed to the actual function. Note that in our default context, we simply wire a bunch of functions to the methods of the built-in Math object.
if (node.hasOwnProperty('FunctionCall')) {
expr = node.FunctionCall;
if (context.Functions.hasOwnProperty(expr.name)) {
args = [];
for (i = ; i < expr.args.length; i += 1) {
args.push(exec(expr.args[i]));
}
return context.Functions[expr.name].apply(null, args);
}
throw new SyntaxError('Unknown function ' + expr.name);
}
What if we want to have a custom function, maybe because it is not supported by the Math object? It can not be easier than defining the function for the context. As an example, let’s implement sum which adds all the number passed in the argument. Since we deal with a function which may have a variable number of arguments, we use special arguments object instead of named parameters:
context.Functions.sum = function () {
var i, total = ;
for (i = ; i < arguments.length; i += 1) {
total += arguments[i];
}
return total;
}
Dead easy, isn’t it?
As with the previous parts, what presented above are various code fragment only, the full working code is available from my TapDigit project. Don’t be scared, the complete implementation of the evaluator is not even 100 lines.
Finally, for the demo, visit ariya.github.io/tapdigit/eval.htm with your favorite browser, smartphones, or tablets.
And that is the end of our adventure! Of course I only cover the basics so far, hopefully now you have a foundation to go and explore the wonderful world of bytecode interpretation, code transpiling, and many more. Don’t forget to have some fun!